clustering
Introduction of various clustering techniques.
PRTools and PRDataFiles should be in the path
Download the m-file from here. See http://37steps.com/prtools for more.
Contents
prwaitbar off % waitbar not needed here delfigs % delete existing figures randreset; % takes care of reproducability prwarning off % no warnings
Define a dataset
we use some standard routines to create 8 two-dimensional clusters. After creation the label information is removed.
randreset; m = 50; a = prdataset(rand(m,2).*repmat([8,0.5],m,1))+repmat([1 -1],m,1); a = [a; prdataset(rand(m,2).*repmat([8,0.5],m,1)+repmat([1.5 0.5],m,1))]; x = +gendats([m m],2,4).*repmat([1,1],2*m,1)+repmat([3 5],2*m,1); a = [a; x]; y = +[gendatc(m); gendatc(m)+repmat([0 10],m,1)]; y = y.*repmat([0.2,0.35],2*m,1)+repmat([-1.5 1.5],2*m,1); a = [a; y]; z = prdataset(+[gencirc(m,0.05)*7; gencirc(m,0.04)*2.5]); z = z.*repmat([0.5,0.5],2*m,1)+repmat([16 3],2*m,1); a = [a; z]; scattern(prdataset(a,genlab(m*ones(1,8)))); axis equal; title('Original dataset'); a = prdataset(+a); % remove labels
Welcome to PRTools5. It is not fully compatible with PRTools4. Go to http://37steps.com/prtools5-intro/ for transition notes or click <a href="http://37steps.com/prtools5-intro/">here</a>. Type 'prnews' to open your browser for PRTools news
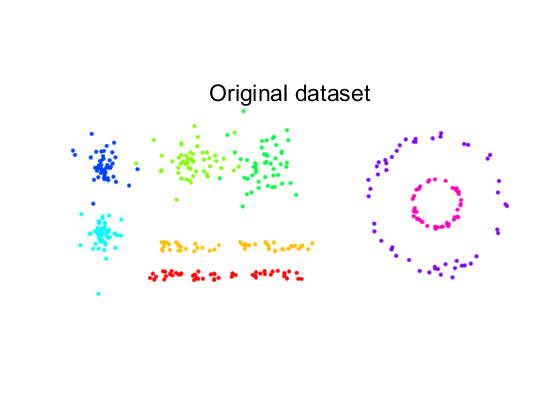
This dataset consist of:
- two straight, noisy lines
- two noisy circles inside each other
- two spherical normal distributions
- two elongated non-normal distributions.
partitional clustering by kmeans, find 8 clusters
figure; [labs,b] = prkmeans(a,8,1,'rand'); subplot(2,2,1); scattern(b); axis equal title('kmeans, iteration 1'); % The cluster labels are stored in labs. The dataset b contains the % original objects, but labeled with the cluster labels after 1 iteration. it = [2 2 100]; for n=1:3 % Here the results after more iterations are computed. Each call is % initialised by the cluster labeling resulting from the previous call. [labs,b] = prkmeans(a,8,it(n),labs); % Note that for n=3 100 iterations are requested. The algorithm, however, % stops much earlier, when the result is stable. subplot(2,2,n+1); scattern(b); axis equal title(['kmeans, iteration ' num2str(it(n)+1)]); end title('kmeans, final result');
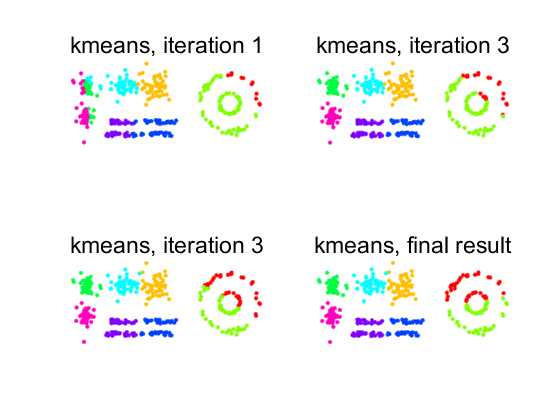
The figure illustrates that the kmeans algorithm creates spherical clusters with the same radius.
hierarchical clustering, dendrograms
The two most extreme versions are shown, single linkage and complete linkage. In this section the densrograms are computed.
figure; d = sqrt(distm(a)); % The routines operate on the distance matrices den = hclust(d,'single'); subplot(2,1,1); plotdg(den); title('single linkage dendrogram'); set(gca,'xtick',[]); % removes the cluttered x-ticks den = hclust(d,'complete'); subplot(2,1,2); plotdg(den); title('complete linkage dendrogram'); set(gca,'xtick',[]); % removes the cluttered x-ticks fontsize(14) % default font size is not nice
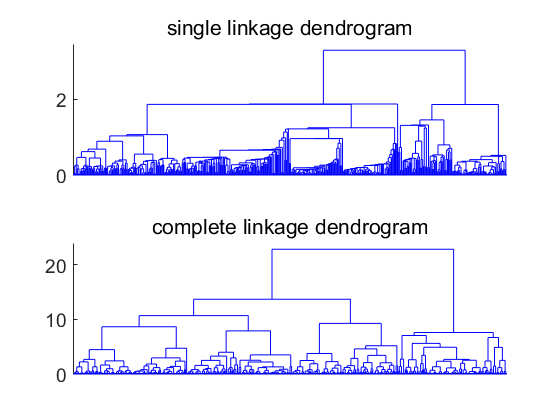
Dendrograms show in the horizontal direction the objects in some order. In the vertical direction the cluster distance is shown when two clusters are merged using the single linkage or complete linkage definition.
The two dendrograms show the very different characteristics of the two procedures. By single linkage clusters grow gradually with more remotely located objects until they are merged with another cluster.
By complete linkage clusters of similar size (largest within distance) are created.
hierarchical clustering, 4 clusters
figure; labs = hclust(d,'single',4); subplot(2,1,1); scattern(prdataset(a,labs)); axis equal; title('single linkage,4 clusters'); labs = hclust(d,'complete',4); subplot(2,1,2); scattern(prdataset(a,labs)); axis equal; title('complete linkage, 4 clusters');
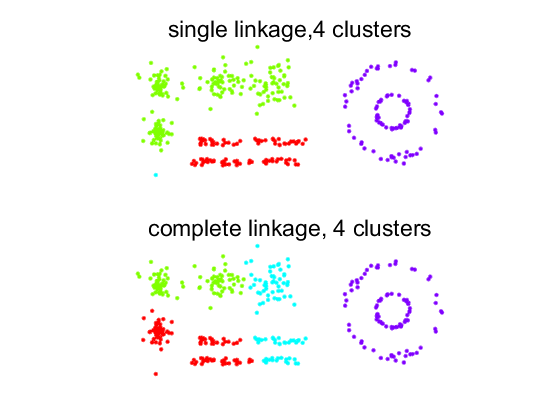
Here the resulting clusterings show their characteristing: elongated clusters constituted by touching (single linkage) or spherically shaped clusters neglecting touching (complete linkage). Note that single linkage shows one cluster of a single object. This can be verified in the dendrogram.
hierarchical clustering, 8 clusters
r = [1 3 5 7 2 4 6 8]'; % trick to shuffle labels for better visualization. figure; labs = hclust(d,'single',8); subplot(2,1,1); scattern(prdataset(a,r(labs))); axis equal; title('single linkage, 8 clusters'); labs = hclust(d,'complete',8); subplot(2,1,2); scattern(prdataset(a,r(labs))); axis equal; title('complete linkage, 8 clusters');
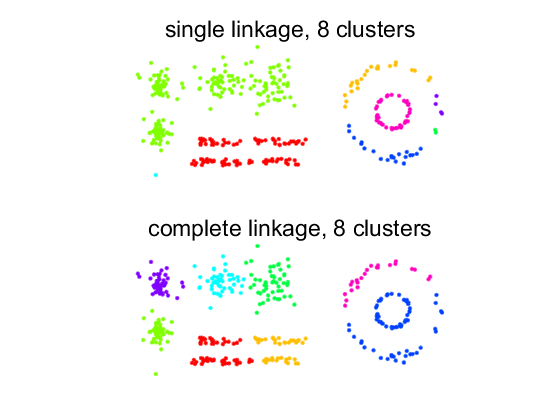
Again: elongated clusters for single linkage and spherical clusters for complete linkage. Single linkage has three single object clusters.
mode seeking
This procedures searches the modes (local maxima) of the density. A nearest neighbor search is used to follow from each object the density gradient to a mode. The number of neighbors used for the search influences the number of clusters found: the more neighbors the less clusters.
figure; labs = modeseek(d,20); subplot(2,1,1); scattern(prdataset(a,labs)); axis equal; title(['mode seeking, 20 neighbors, ' num2str(max(labs)) ' clusters']); labs = modeseek(d,10); subplot(2,1,2); scattern(prdataset(a,labs)); axis equal; title(['mode seeking, 10 neighbors, ' num2str(max(labs)) ' clusters']);
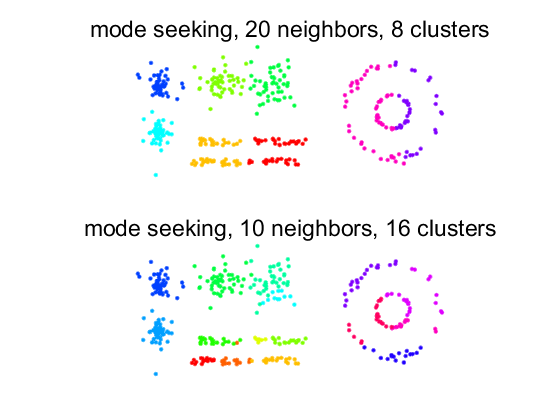
For larger numbers of neighbors, clusters are combined as long as objects have neighbors in the other cluster having a higher density.